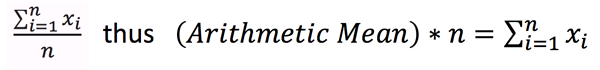“Whenever the market has volatility we lose money. We call this ‘volatility drag.’”
“Price fluctuations create a continual drag on your portfolio growth.”
“The more volatile our year-to-year returns, the less money we actually have. . . . We call this the ‘volatility drag.’ I also like to call it the volatility tax.”
— Creekside Partners
“An investment with 10% volatility faces a drag on return of 0.50%. . . . The drag grows quickly as volatility increases.”
— Paul Bouchey, CFA; Vassilii Nemtchinov; Alex Paulsen; and David M. Stein
Scary stuff! But reading these articles, I found myself wondering, is it actually true? Like so many myths, there is a kernel of truth. But the interpretation that volatility is an active force, “pulling” down returns and costing you money, is simply not correct.
In Part 1, we will explore the crux of the issue, understanding the geometric mean. In Part 2, we will apply this understanding to arguments for volatility drag.
Where—Force Art Thou?
Remember free-body diagrams from physics class, the drawings of an object with arrows representing the forces? Drag was a common force, present when an object moved through a medium like air or water. So where does the “volatility drag” force come from? What medium is it that prices move through?
The proposition is that the difference between the geometric mean and the arithmetic mean of a series of returns represents “drag.” Let us revisit the geometric mean, and perhaps we can find a force. (The geometric mean is often encountered in the form of compound annual growth rate (CAGR). CAGR is a special case of geometric mean, useful when the initial value and ending value for n periods are known.)
To motivate the discussion, let’s look at an example of past performance data on a mutual fund prospectus that makes use of the geometric mean to calculate the “average annual total return.”
Average Annual Total Return
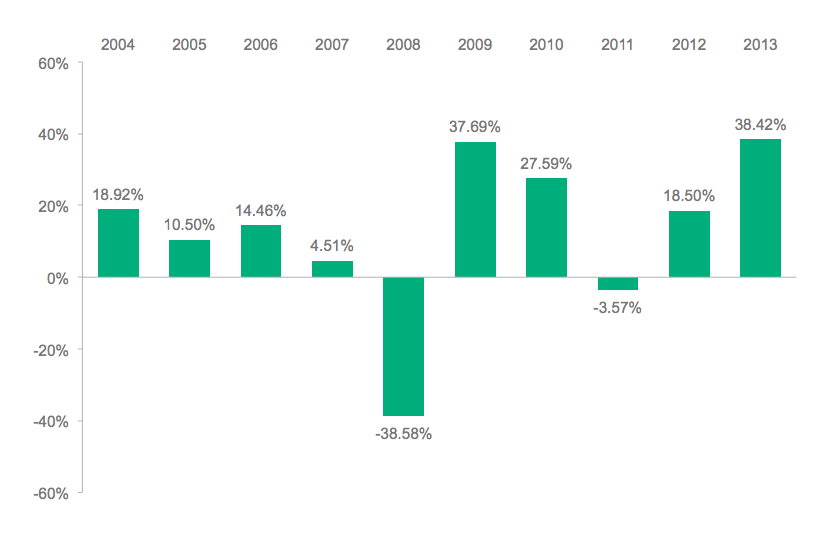
If you have read a mutual fund prospectus, then you have seen a chart similar to the following one, showing the annual total returns for the previous 10 years.
Annual Total Returns — Vanguard Extended Market Index Fund Institutional Shares
The percent returns are the year-over-year numbers and are straightforward. These charts are accompanied by a table that includes average annual total returns for one, five, and 10 years.
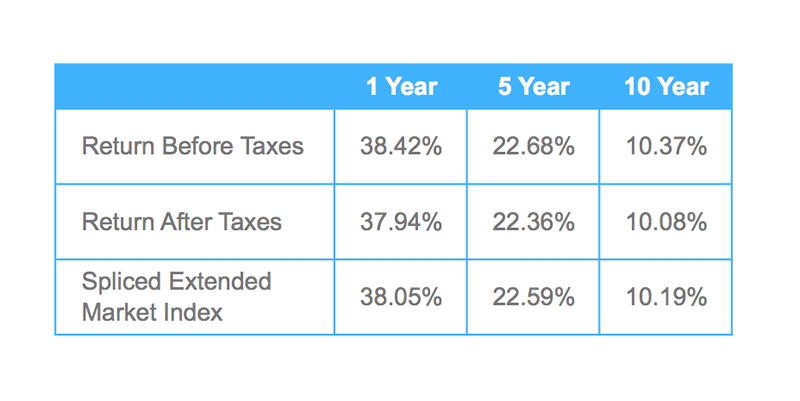
Average Annual Total Returns for Periods Ended 31 December 2013
Here we must be a little cautious: This use of average is not the most common usage. In most cases, when we see the term average, we add up the numbers and divide the total by the number of elements. A quick check with the five-year return before taxes, calculating the usual average, is 23.75%. But the table says 22.68%. That is because there is more than one type of average, or mean, and in this case the geometric mean is the appropriate one to use. So why is it “appropriate”?
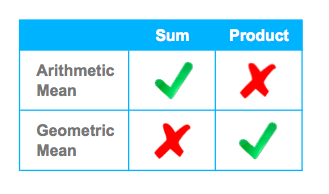
Means: A Quick Refresher
The arithmetic mean is the one with which we are most familiar. It is a property of sums: 2 + 8 is a sum of two elements. The one value that relates the number of elements to the sum of the elements is the arithmetic mean.
2 + 8 = 10 and the arithmetic mean is 10/2 = 5
The geometric mean is the analogous property for products. 2 * 8 is a product of the same two elements. The value that relates the number of elements to the product of the elements is the geometric mean.
Yes, and we can find it with the square root. √16 = 4. This is the geometric mean.
What if we had three elements? Say 2 + 8 + 32= 42. The arithmetic mean is 42/3 = 14.
Now try 2 * 8 * 32 = 512. We have three numbers, so need a cubed root: ∛512 = 8
 In general, the arithmetic mean is defined as:
In general, the arithmetic mean is defined as:
The geometric mean is defined as:
Back to the Prospectus
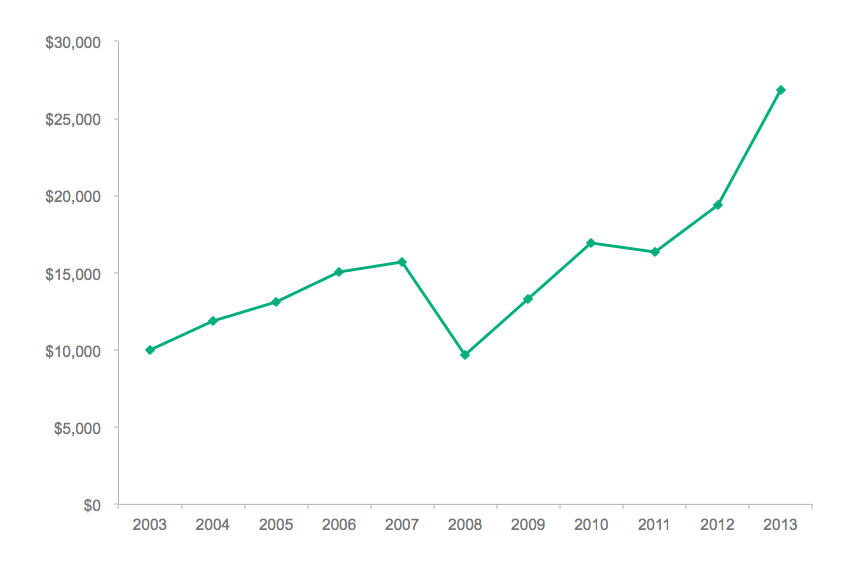
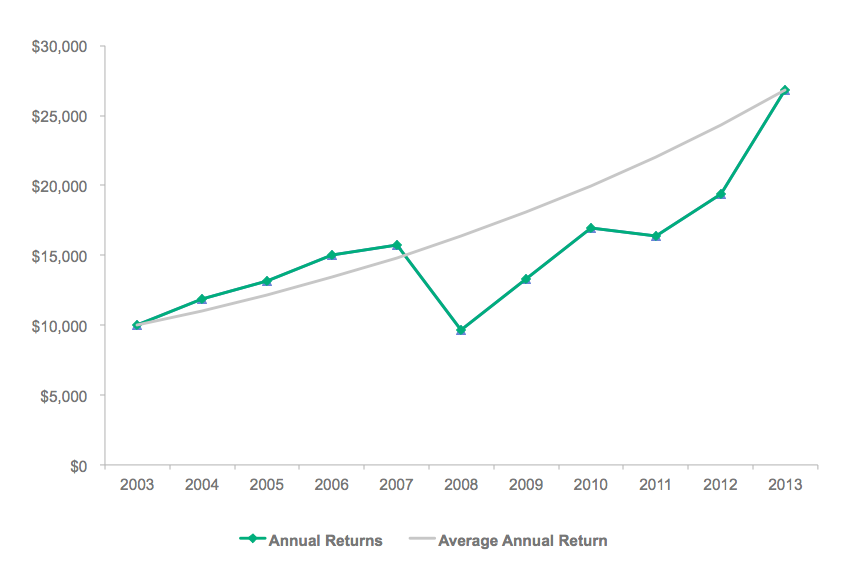
Another chart you may see on a prospectus or fact sheet is the growth of a hypothetical investment using the annual returns.
Hypothetical $10,000 Investment
Can we calculate the final value using only the returns?
The initial value multiplied by 1 plus each of the annual returns in decimal form will get us there. (For more information on where the 1 came from and on logarithms in general, this article provides a good primer.)
This Is a Product, Not a Sum
$10,000 * 1.1892 * 1.105 * 1.1446 * 1.0451 * 0.6142 * 1.3769 * 1.2759 * .9643 * 1.1850 * 1.3842 = $26,828
As we discussed in the section above, the geometric mean is the average to use on a product. So, the geometric mean of the returns xi over 10 years is ![]() or a 10.37% annualized return, which matches what we were given in the table! With this value, we can calculate the ending value directly: $10,000 * 1.1037^10 = $26,828. The average annual return also lets us calculate the value for the intermediate years, as if there was an investment that earned exactly the average annual return every year. This is plotted below, showing a smooth curve that starts and ends at the same points.
or a 10.37% annualized return, which matches what we were given in the table! With this value, we can calculate the ending value directly: $10,000 * 1.1037^10 = $26,828. The average annual return also lets us calculate the value for the intermediate years, as if there was an investment that earned exactly the average annual return every year. This is plotted below, showing a smooth curve that starts and ends at the same points.
Hypothetical $10,000 Investment
What about Log Returns, Are They Related?
Yes! One property of logarithms is that they transform a product to a sum: log(a * b * c) = log(a) + log(b) + log(c). Once transformed to a sum, the arithmetic mean applies. Taking the arithmetic mean of the log returns and then converting it back to the standard form is equivalent to the geometric mean. (In this context, a, b, and c would represent “1 + return.” We will call “log(1+return)” the “log return.”)
This is a regularly used approach, sometimes mandated by regulators, to calculate average periodic returns. Using the previous set of returns and calculating their log-returns (using log10):
Noting that 10.37% is the same value we determined above, we can see the two approaches are equivalent.
Summing Up
Now when statements are made regarding the average return, we can ask a few questions. What kind of average? If it’s from a series of chained returns (i.e., a product), are they talking about arithmetic mean of log returns? Are they talking about the geometric mean of the returns? If neither of these is the case, we must examine the conclusions more closely.
“Volatility drag” is one such conclusion. We found that the arithmetic and geometric means are related — both are equations using the same set of numbers — but the difference between them is in the definition, not from a force. Why, then, is this such a persistent myth? There are two seductive arguments made in its favor. One is very simple and appeals to our intuition, but contains a flawed assumption. The other stems from a slight misinterpretation of terms in a widely used mathematical model of prices.
Using the language of arithmetic and geometric means developed here, we will look at these two arguments in the next post and consider some of the practical ramifications.
All posts are the opinion of the author. As such, they should not be construed as investment advice, nor do the opinions expressed necessarily reflect the views of CFA Institute or the author’s employer.
Copyright © Will Morrison, CFA Institute